If You Compared The Allele Frequencies In The Two Populations, What Would You Expect To Find?
Allele frequencies (or percentages, if you prefer) in a population will remain in Hardy-Weinberg Equilibrium (HWE) from generation to generation if the following assumptions are met:
- Natural option is not occurring
- Migration (Gene Flow) is not occurring
- Mutation is not occurring
- Genetic Drift is not occurring (drift is less likely in populations of big size)
- Mating occurs at random
Although these assumptions are rarely truthful in the natural globe, they permit us to summate an expected allele frequency. Significant differences between the observed and expected frequencies bespeak that "something" (i.e. ane or more than of the to a higher place) is going on, and therefore tell united states that "microevolution" is occurring.
Calculating Expected Allele and Genotype frequencies:
In the simplest possible situation we take a single gene with only ii alleles. These alleles might be A and a, or A1 and A2. Let's say that A or A1= tall, and a or Aii= short. Don't worry for at present whether the alleles are dominant and recessive or co-dominant. They will have frequencies p and q in a population. (Because there are only two possibilities and they have to add upwards to 100%, p + q = 1.)
If we know the allele frequencies, we can predict the genotype frequencies. The expected genotype frequencies of the two alleles are calculated every bit shown. This ought to look familiar: information technology'southward our sometime friend the Punnet'due south Square. Allele A or Aone has a frequency of p, and allele a or A2 has a frequency of q. Multiply the allele frequencies to the get the probability of each genotype.
| Allele | A | a | |
| Frequency | | | |
| A | | | |
| a | | | |
| Allele | A1 | A2 | |
| Frequency | | | |
| A1 | | | |
| A2 | | | |
In other words, p2 + pq + pq + qtwo = one, or 100%. The expected frequencies of the genotypes are therefore:
| | |
| | |
| | |
| | |
Let's take a look at some graphs of this to brand it a piffling easier to see. For values of p from 0 to 1, in intervals of 0.1, here's what we get:
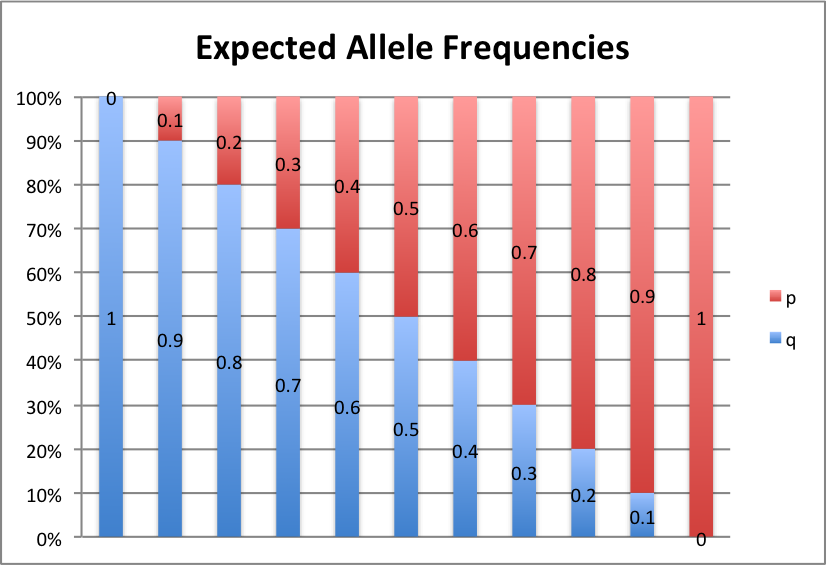
p+q=1, so p=i-q and q=1-p
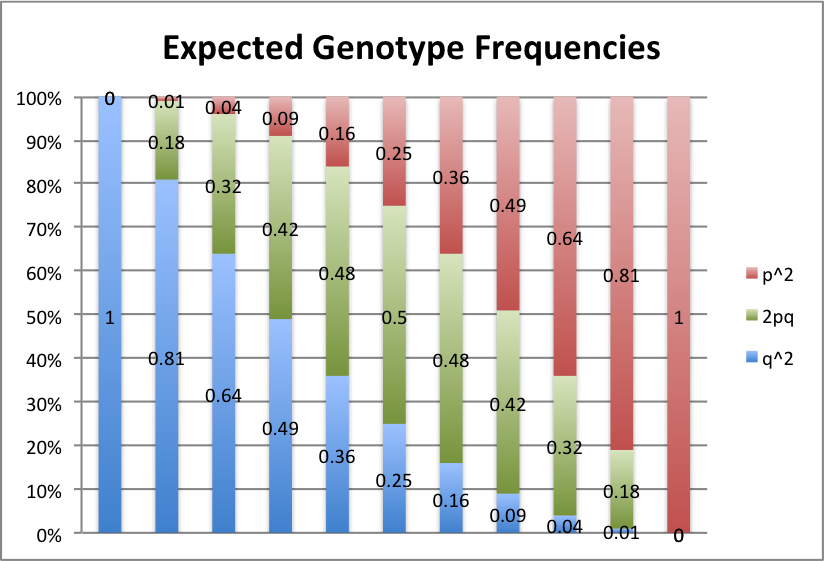
Blood-red represents the frequency of the AA or AaneAone genotype, green is the Aa or A1A2 genotype, and bluish is the aa or AtwoA2 genotype.
All of the to a higher place has to exercise with the allele and genotype frequencies we would expect to see. Next, permit's await at the real world situation so we can compare.
Calculating Observed Allele and Genotype Frequencies:
In a existent globe population, nosotros can but see phenotypes, not genotypes or alleles. Even so, in a population of genotypes AA, Aa and aa, the observed frequency of allele A equals the sum of all of the AA genotype plus half of Aa genotype (the A half). The observed frequency of allele a is therefore one-half of the Aa individuals (the a half) plus all of aa individuals. If you know one value, y'all can of course just subtract it from 1 (100%) to become the value of the other. In other words, the observed frequency of A = 100%(AA) + 50%(Aa) and a = l%(Aa) and 100%(aa)
| Phenotype | | Makeup | Frequency |
| Tall | | 100% A | p2 |
| Tall | | 50% A and fifty% a | 2pq |
| Brusque | | 100% a | q2 |
| Phenotype | | Makeup | Frequency |
| Tall | | 100% Aane | pii |
| Medium | | l% A1 and 50% Atwo | 2pq |
| Brusk | | 100% A2 | q2 |
Tip: If the alleles are codominant, each phenotype is distinct (y'all can distinguish between tall, medium and short) and your job is easier. If the alleles are dominant and recessive , we tin can't visually tell the homozygous AA from the heterozygous Aa genotypes (both are alpine), so it's best to get-go with the homozygous recessive (short) aa individuals. Count up the aa types and y'all have the observed q2. And then, take the square root of q2 to get q, and then subtract q from i to get p. Square p to get p2 and multiply 2*p*q to get the observed heterozygous Aa genotype frequency.
Conclusion:
If observed and expected genotype frequencies are significantly different, the population is out of HWE.
| Genotype Frequencies | |||
| AA | Aa | | |
| Observed | | | |
| Expected | | ||
| Difference | | | |
| Genotype Frequencies | |||
| A1Aane | A1A2 | | |
| Observed | | | |
| Expected | | ||
| Departure | | | |
Question: Why might observed and expected phenotype frequencies differ? Imagine the following scenarios where natural selection is at work. Situation one favors simply one tail of the distribution. Perhaps the tallest, perchance the shortest, just not both. This is directional selection. Now imagine that both tails of the distribution are selected against, and only the eye is favored. This is chosen stabilizing selection. Next imagine that the extremes on both ends are favored. This is called disruptive selection. In each of these scenarios, what would happen over time?
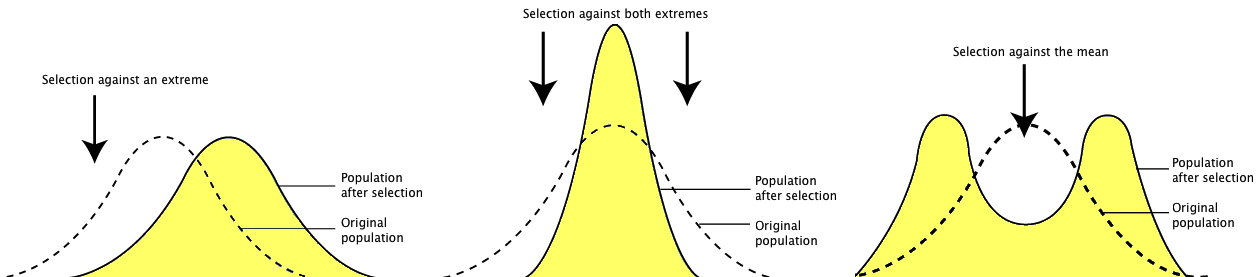
Before (dotted line) and after (yellow shaded area) directional selection, stabilizing selection, and disruptive selection.
Examples:
One common misconception is that dominant alleles will ascent in frequency and recessive alleles will reject in frequency over fourth dimension. In reality, allele frequencies will non modify from one generation to the adjacent if the assumptions listed in a higher place are non violated. A good instance of this is human ABO blood type. Type O blood is recessive merely it remains the most common.
In the hwe.xlsx Excel Spreadsheet, there are three examples to help make this more physical.
Case 1: Allele A is dominant and allele a is recessive. Ready the original frequencies of p (allele A) and q (allele a) at 0.six and 0.iv in Generation 1. These are highlighted in blue. All other numbers are calculated from these two original data points. The frequency of genotype AA is determined by squaring the allele frequency A. The frequency of genotype Aa is adamant by multiplying two times the frequency of A times the frequency of a. The frequency of aa is determined by squaring a. Endeavour changing p and q to other values, ensuring only that p and q ever equal 1. Does information technology make whatever departure in the results?
Example 2: Alleles A1 and Aii are co-ascendant. In this case, A1 is at a frequency of 0.25 and A2 is at a frequency of 0.75.
Example 3: Alleles A and a are dominant and recessive. Annotation that allele A is at very low frequency despite existence ascendant. Does it increment in frequency?
Problem:
The second sometimes confusing matter nearly HWE is that after all of the examples above, yous may wonder if it is possible for the observed and expected frequencies to differ. Here'southward an example where they do:
In a population of snails, beat out color is coded for by a single gene. The alleles Ai and Aii are co-dominant. The genotype AoneA1 makes an orange shell. The genotype A1Atwo makes a xanthous shell. The genotype A2 A2 makes a blackness shell. 1% of the snails are orange, 98% are yellow, and ane% of the snails are black.
p2 = Expected frequency of AoneAi = 0.25
2pq = Expected frequency of AoneA2 = 0.fifty
q2 = Expected frequency of A2 A2 = 0.25
| Phenotype | Orange | Yellowish | Black |
| | | | |
| | | | |
| Expected | | | |
| | | | |
At that place are significantly fewer orange and black snails than expected, and significantly more than yellow snails than expected. Information technology appears that this is a case of stabilizing selection, since both tails announced to be strongly selected against.
Source: https://www2.nau.edu/lrm22/lessons/hwe/hwe.htm
Posted by: beasleyluxual1965.blogspot.com

0 Response to "If You Compared The Allele Frequencies In The Two Populations, What Would You Expect To Find?"
Post a Comment